La numérisation

Cet article a pour but de présenter les bases de la conversion analogique-numérique à ceux qui le souhaitent. Afin de transformer un signal analogique en signal numérique, il est nécessaire de passer par une succession d'étapes qui vont permettre d'assurer le bon fonctionnement du procédé. Dans un premier temps, il va falloir échantillonner le signal, c'est-à-dire le transformer en une série d'échantillons de valeurs. Puis il faudra le filtrer pour isoler la partie du signal qui nous intéresse. Enfin, il faudra attribuer à chaque échantillon une valeur numérique.

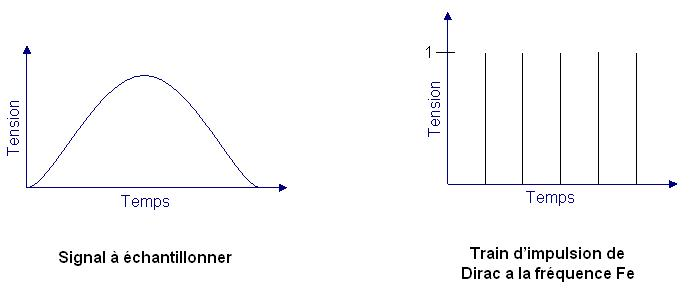
La manipulation informatique des signaux impose leur transformation en valeurs numériques. Cette transformation se fait généralement par prélèvements d'échantillons réalisés à une fréquence Fe appelée fréquence d'échantillonnage. Pour réaliser cette « prise » d'échantillons, on multiplie le signal analogique par ce que l'on appelle un train d'impulsion de Dirac :

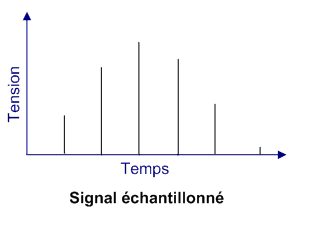
Plus la fréquence d'échantillonnage sera grande plus la mesure sera précise et plus le signal pourra être restitué fidèlement. Mais cela demande un espace mémoire important, car le nombre de données à traiter sera énormément augmenté.

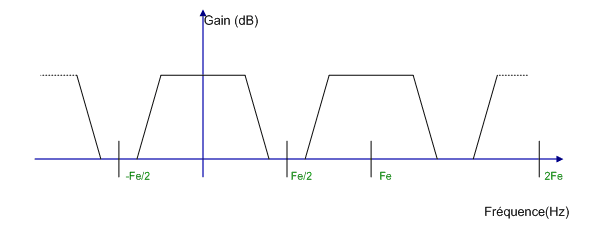
Lorsque l'on fait l'analyse de Fourier d'un signal échantillonné, il apparait qu'une infinité de spectres sont créés, centrés autour des différents multiples de la fréquence d'échantillonnage (Fe, 2Fe, 3Fe, etc.).

Ce phénomène implique donc un rapport entre la fréquence d'échantillonnage et la fréquence du signal à échantillonner, il s'agit de la condition de Shannon :
La fréquence d'échantillonnage doit être supérieure au double de la plus haute fréquence contenue dans le signal à échantillonner.

Fe > 2 * fréquence du signal

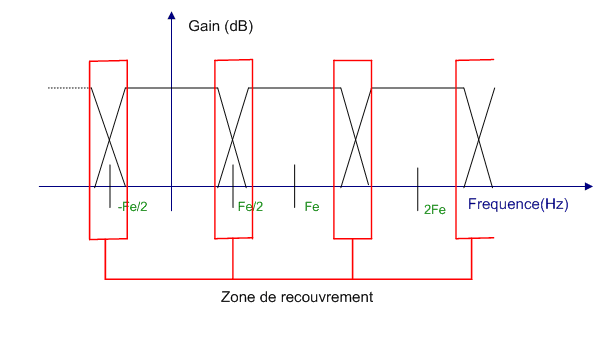
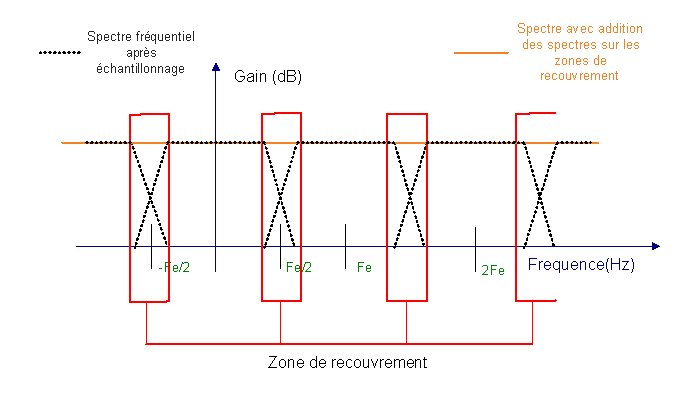
Si la condition de Shannon n'est pas respectée, les différents spectres se croisent et au niveau des zones de recouvrement, les spectres s'additionnent ; on appelle cela un repliement spectral (ou aliaising). Le spectre restitué après filtrage ne correspond donc plus au spectre réel du signal et les analyses en sont faussées :

On constate alors une modification nette et radicale du spectre fréquentiel du signal d'origine rendant impossible la restitution dudit signal.

Une fois le signal échantillonné, il faut se débarrasser des composantes inutiles. En effet les spectres créés autour des différents multiples de la fréquence d'échantillonnage ne nous intéressent pas. Pour se faire, on utilise en général un filtre passe-bas analogique dont la fréquence de coupure Fc est inférieure à Fe/2.

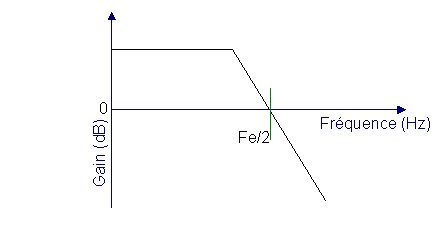
Ainsi tous les signaux dont la fréquence est supérieure à Fe/2 seront fortement atténués.

La quantification
La quantification va attribuer à chaque échantillon une valeur numérique selon un principe de proportionnalité. Ainsi, tout convertisseur analogique-numérique (communément appelé CAN) a besoin d'une valeur de référence (en général la masse) et d'une valeur seuil qui sera choisie en fonction de la précision voulue. Par exemple si on a un convertisseur 16 bits, qu'on utilise la masse comme référence et 5V comme valeur du seuil, on aura une précision de 5/(65536)=76µV ce qui veut dire qu'une variation d'une unité numériquement parlant équivaudra a une variation analogique de 76 µV. (Rappel: 65 536 = 2 puissance 16 = nombre de valeurs possibles avec 16 bits.)
La qualité du signal

Deux facteurs vont jouer sur la qualité du signal :

• la fréquence d'échantillonnage : en effet, plus elle sera élevée plus le signal numérisé sera fidèle au signal analogique initial. À surveiller tout de même, car une fréquence trop élevée demandera un espace mémoire très important ;
• le nombre de bits sur lequel on code les valeurs qui va nous donner le nombre de valeurs que peut prendre un échantillon et la précision en fonction de la valeur seuil.

Pour conclure, je dirai que la numérisation peut garantir la qualité d'un signal ou la réduire volontairement, car elle permet de :

• diminuer le coût de stockage ;
• d'effectuer une plus grande variété de traitements ;
• de tenir compte du nombre de valeurs nécessaires selon l'application (par exemple sur un signal vidéo noir et blanc, il s'agirait du nombre de nuances de gris) ;
• de tenir compte des limitations mémoires et termes de mémoire et de vitesse de calcul.

Malgré tout, il est nécessaire de tenir compte de certains paramètres. En effet, un mauvais choix de la fréquence d'échantillonnage peut complètement déformer le signal d'origine ou nécessiter un espace mémoire conséquent, ce qui dans certains cas peut devenir handicapant.

• Le fonctionnement que j'ai décrit dans cet article est un fonctionnement « idéal », c'est-à-dire qu'il ne tient pas compte des réalités des signaux. Par exemple, réaliser un signal d'horloge parfait est impossible, on ne sait pas le faire. Il y a donc toujours un léger décalage (appelée Jitter) entre l'horloge théorique et l'horloge réelle qui, lors de l'échantillonnage, va très légèrement modifier le spectre fréquentiel… Cette modification est si infime que l'on considère en général que les évènements ont tout de même été parfaitement échantillonnés.
• Attention : les composants appelés CAN (ou Convertisseur Analogique Numérique) réalisent les deux étapes que sont l'échantillonnage et la quantification, mais la quantification n'est pas parfaite. Comme je l'ai expliqué plus haut une quantification est une opération de proportionnalité or la courbe de quantification d'un CAN n'est pas linéaire, d'où la nécessité de s'assurer une marge d'erreur lorsque l'on choisit le quantum (la précision) de l'opération.

• aliasing : phénomène de repliement du spectre lorsque la condition de Shannon n'est pas respectée.
• analyse de Fourier : le but d'une analyse de Fourier et de décomposer un signal complexe en une somme de sinusoïdes afin d'étudier son comportement en fréquence et ses caractéristiques. Les résultats de cette analyse se retrouvent généralement sous forme de spectres (graphiques) fréquentiels.
• Filtre analogique passe-bas : il s'agit d'un petit montage électronique permettant d'atténuer fortement tout signal ayant une fréquence supérieure à Fc (appelée fréquence de coupure).

Il y a plusieurs personnes que j'aimerais remercier.

• Matthieu Brucher pour l'aide précieuse qu'il m'a apportée dans le contenu de cet article et dans son édition.
• buchs pour son aide concernant la structure et l'édition de cet article.
• djo.mos pour la relecture.